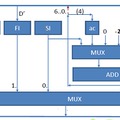
Let us have a look at some elementary functions and predicates to have a better look and feel how FunCPU works. The definitions of these objects will be suppmented with their assembly code counterparts written directly in FunCPU machine code.
In the subsequent section, the following encoding is used:
FC - increment function
FD - if-then-else
FE - decrement function
FF - end of expression
Identity function
I(x):= x
7F FF
Constant function
C(x):= c
„c” FF, where c=00..7B
Please note that as 7C and above, up to 7F denote arguments, therefore it is impossible to write a constant function directly, which returns these values. For example, as we have seen 7F FF denotes the one-argument identity function.
Fortunately we can overcome this limitation by defining the function "7C FF" as follows:
FC 7B FF
That is, essentially, incrementing the value 7B to get the 7C.
Or analogously,
FE 00 FF
represent the constant function 7F.
Please note this will work, as functions will be evaluated by unfolding the function definition and inserting into the expression memory. In the expression memory no distinction is made between constants and arguments, they are all being treated in the same way.
Few Predicates
not(x):= if x then 1 else 0
FD 7F 7E 81 FE 7E FE 7F FF
Assuming that "=" definition is stored at address 00.
>(x,y):= if x=0 then not(y) else >(dec(x),dec(y))
FD 7E 88 7E 91 FE 7E FE 7F FF
Assuming further, that "not" and ">" definitions are stored at 10 and 20 respectively.
Some functions
add(x,y):= if y=0 then x else inc(add(x,dec(y)))
FD 7F 7E FC 81 7E FE 7F FF
Assuming that "add" is stored at 00.
mul(x,y):= if y=0 then 0 else add(x,mul(x,dec(y)))
FD 7F 00 81 7E 91 7E FE 7F FF
Assuming that "mul" is stored at 20.
fac(n):= if n=0 then 1 else mul(n,fac(dec(n)))
FD 7F 01 81 7F 98 FE 7F
Assuming that "fac" is stored at 30.
As one can see, a whole set of interesting and useful functions and predicates can be built, one based on another. So the three atomic functions along with the potential of user defined functions and (recursive) function calls make it possible to define arbitrary complex functions (in theory, in reality memory constraints put limitation on the set of definable functions).
A more complex function is the Ackermann function, which is recursive, but not primitive recursive.
ack(m,n):=
if m=0 then inc(n)
elsif n=0 then ack(dec(m),1)
else ack(dec(m),ack(m,dec(n)))
FD 7E FC 7F FD 7F 81 FE 7E 01 81 FE 7E 81 7E FE 7F FF
where "ack" is defined at location 00.
We can already "feel" that the FunCPU is Turing-complete...